In this edition, we are going to look at a cool math trick for generating sinewaves. The code is for the SX processor but can be converted to PIC or other common embedded processors without much trouble.
Before your eyes glaze over on the math part, know that there are some good things to learn here. One is how complex math functions can get compressed into a few cycles of embeded controller code by looking at how the function output changes for very small changes in the input. When you can start with a correct value and concentrate on looking for a small adjustment, you can often "throw away" large parts of the function. The article inside this edition is a perfect example of that.
Secondly, there is some good code that shows how doing an addition or subtraction can involve just toggleing ONE BIT.
Read on!
First let me show you some very nice table based code for generating sine waves from Peter Van der Zee. This was an example for the Prototyping Board for the SX28 that Peter entered in the Parallax Design Contest
Sine2 ;calculate lookup time for generator 2, and if so, get sine value decsz Period2 ;step frequency 2 period duration retp ;not time for next sine lookup; return to scheduler mov Period2,Period2Load ;reload period 2 timer inc F2index ;step to next sine value in lookup table mov w,F2index ; call SineLookup ;get sine value for this index mov Dac2Value,w ;setup new dac 2 value for the ISR retp ;done freq2; return to scheduler SineLookup ;lookup the sine value of index in w and w,#%0000_1111 ;only use 16 steps in lookup table add pc,w ;calculate offset into lookup table Sin0 retw 128 ;$80 Sin1 retw 177 ;$b1 Sin2 retw 218 ;$da Sin3 retw 245 ;$f5 Sin4 retw 255 ;$ff Sin5 retw 245 ;$f5 Sin6 retw 218 ;$da Sin7 retw 177 ;$b1 Sin8 retw 128 ;$80 Sin9 retw 79 ;$4f SinA retw 38 ;$26 SinB retw 11 ;$b SinC retw 1 ;$1 SinD retw 11 ;$b SinE retw 38 ;$26 SinF retw 79 ;$4f
It works fine for most applications, but as you can see, the result is a stepped approximation of a sine that does not increase in detail as the step size (the number of degrees per new output value) decreases. If you are putting out a new value every time through the loop, incrementing the table pointer, then the result is no worse than any other method. But if you are using the same value several time in a loop, the result is a jerky approximation of a sine.
This table based method is great for generating sinewaves that do not change in frequency and will be heavily filtered such as AC inverters, 3 phase power generation or that are fairly high frequency like Modem tones. But when you need to vary the frequency of the output, or get a smoother waveform you need something more.
You could just include a larger table, with an entry for every value you need in the slowest sine you will generate and then skip entries in the table to generate higher frequencies. Other methods include the use of "interpolation" where the values between the actual entries in a smaller table are approximated in a linear fasion. But... there is a better way which I found while thumbing through my collection of old Byte Magazines.
Robert Grappel 148 Wood St Lexington MA 02173
The instruction set of a typical 8 bit processor can be quite confining at times. Any task requiring more than simple integer addition and subtraction can become a nuisance. There are reference books from which multiplication and division routines can be obtained, and square root and. other functions can be built by using expansion, iteration, or other well-known methods. Implementing these algorithms on a microprocessor uses much space and programming time. Trigonometric functions are among this class of
Difficult functions. However, if one can tolerate accuracy of one part in 100, and allow about 1 ms per computation, the routine described in this article will provide sine and cosine values in a very simple 40 byte routine. I have coded it for a Motorola M6800 processor but it could easily be converted to any other processor.
The algorithm is based on two trigonometric identities:
sine(Ø+s) = sin(Ø)cos(s) + cos(Ø)sin(s)
cos(Ø+s) = cos(Ø)cos(s) - sin(Ø)sin(s)
where Ø is the angle we are interested in and s is a small step in angle added to Ø. If we make the step small enough, we can approximate sin(s) and cos(s) as follows:
sin(s) = s
cos(s) = 1
Combining these four equations we get:
sin(Ø+s) = sin(Ø) + s cos(Ø)
cos(Ø+s) = cos(Ø) - s sin(Ø)
Solving for sine and substituting into the cosine formula:
cos(Ø+s) = (1+s^2)cos(Ø) - s sin(Ø+s)
Since s is very small, we can neglect s^2 and write:
cos(Ø+s) = cos(Ø) - s sin(Ø+s)
Given that we have values for sin(Ø) and cos(Ø) at some point, we can get to any other angle by stepping through the two approximations, first computing sin(Ø+s) and then using that to compute cos(Ø+s). We choose to start at Ø equal to zero, and set cos(Ø) to the largest positive value that can be stored as a signed byte without causing overflow when negated and decremented.
Hence cos(Ø) = 126. Similarly the sin(Ø) = 0.
The step size is chosen to be 0.0625 radian or about 3.58'. The step size must be a binary fraction so that all the multiplication involved in the equations can be performed by arithmetic shifts. If more accuracy is needed, the step size is easily reduced by introducing more shifts into the algorithm.
The assembly code program for the Motorola 6800 version of the routine is shown in listing 1. When called with the angle stored in variable THETA, it returns the sine and cosine of that angle. The accuracy is quite good for angles less than pi()/2 radians (90 degrees). For angles larger than pi()/2 radians, other trigonometric identities can be used:
sin(Ø) = cos(pi()/2-Ø) = sin(pi()-Ø)
cos(Ø) = sin(pi()/2-Ø) = (-cos(pi()-Ø))
Thus, the sine and cosine of any angle can be computed from the values over the range 0 to pi()/2 radians. These identities can be coded quite easily.
All the other trigonometric functions can be computed from the values of sine and cosine. All that is needed is an integer division routine such as the following:
cosec(Ø) = 126/sin(Ø)
sec(Ø) = 126/cos(Ø)
tan(Ø) = sin(Ø)/cos(Ø)
cot(Ø) = cos(Ø)/sin(Ø)
Be careful of overflows and division by zero problems.
This algorithm can perform other tricks. It can generate continuous sine waves of any desired amplitude, period, or phase. Coupled with a digital to analog converter, it could form part of a modem or synthesizer. It could simulate mixers, AM or FM modulators, meyers, etc.
The maximum frequency it can generate depends on the processor cycle time. A 6800 processor running with a 1 MHZ clock could generate a 200 Hz sine wave since there are about 50 machine cycles per step, and about 100 steps per wave. Increasing the step size to 0.125 radians would increase the maximum frequency to about 500 Hz. A step size of 0.25 radians would yield a maximum frequency of nearly 1050 Hz.
I hope that this algorithm will help programmers solve problems involving trigonometric functions, and that applications for microcomputers will expand into new areas where these functions are usefull.
Op
Location Code Operand Label assembly Code
* SUBROUTINE TO COMPUTE SINE AND COSINE
* AS SINGLE-BYTE INTEGERS (SIGNED)
* STEP SIZE OF 1/16 RADIAN OR 3.58 DEGREES
* ACCURACY OF ABOUT 1% FOR RANGE 0
* THROUGH 90 DEGREES
*
0000 THETA RMB 1 *ARGUMENT TO FUNCTION
0001 SINE RMB 1 *SINE OF THETA
0002 COSINE RMB 1 *COSINE OF THETA
0003 86 7E START LDA A #126 *began initialization
0005 B7 0002 STA A COSINE
0008 7F 0001 CLR SINE
OOOB B6 0000 LDA A THETA
OOOE F6 0002 LDA B COSINE *COMPUTE NEW SINE
0011 57 CYCLE ASR B
0012 57 ASR B
0013 57 ASR B
0014 57 ASR B
0015 FB 0001 ADD B SINE
0018 F7 0001 STA B SINE
OO1B 57 ASR B *COMPUTE NEW COSINE
001C 57 ASR B
001D 57 ASR B
001E 57 ASR B
001F F0 0002 SUB B COSINE
0022 50 NEG B
0023 F7 0002 STA B COSINE
0026 4A DEC A
0027 2C E8 BGE CYCLE *LOOP UNTIL DONE
0029 39 RTS
Listing 1: 6800 routine for computing sines and cosines over the range 0 to
pi/2 radians (0 to 90 degrees).
170 April 1979 BYTE Publications Inc
Useing a spreadsheet to collect the results of the algorithm and compare it to the "real" value (as defined by MS Excel) shows that it does pretty well. Email me if you want the spreadsheet.
Step |
Radians |
Degrees |
sin() |
~sin() |
error |
cos() |
~cos() |
||
| 0 | 0.0000 | 0.00 | 0.0000 | 0 | 0% | 126.0000 | 126 | Range: |
126 |
| 1 | 0.0625 | 3.58 | 7.8699 | 7 | -1% | 125.7540 | 126 | Divisor: |
16 |
| 2 | 0.1250 | 7.16 | 15.7090 | 14 | -1% | 125.0169 | 126 | Step: |
0.0625 |
| 3 | 0.1875 | 10.74 | 23.4868 | 21 | -2% | 123.7916 | 125 | ||
| 4 | 0.2500 | 14.32 | 31.1729 | 28 | -3% | 122.0830 | 124 | ||
| 5 | 0.3125 | 17.90 | 38.7373 | 35 | -3% | 119.8976 | 122 | ||
| 6 | 0.3750 | 21.49 | 46.1503 | 42 | -3% | 117.2440 | 120 | ||
| 7 | 0.4375 | 25.07 | 53.3832 | 49 | -3% | 114.1325 | 117 | ||
| 8 | 0.5000 | 28.65 | 60.4076 | 56 | -3% | 110.5754 | 114 | ||
| 9 | 0.5625 | 32.23 | 67.1961 | 63 | -3% | 106.5865 | 111 | ||
| 10 | 0.6250 | 35.81 | 73.7223 | 69 | -4% | 102.1814 | 107 | ||
| 11 | 0.6875 | 39.39 | 79.9605 | 75 | -4% | 97.3772 | 103 | ||
| 12 | 0.7500 | 42.97 | 85.8865 | 81 | -4% | 92.1928 | 98 | ||
| 13 | 0.8125 | 46.55 | 91.4771 | 87 | -4% | 86.6484 | 93 | ||
| 14 | 0.8750 | 50.13 | 96.7105 | 92 | -4% | 80.7656 | 88 | ||
| 15 | 0.9375 | 53.71 | 101.5662 | 97 | -4% | 74.5674 | 82 | ||
| 16 | 1.0000 | 57.30 | 106.0253 | 102 | -3% | 68.0781 | 76 | ||
| 17 | 1.0625 | 60.88 | 110.0704 | 106 | -3% | 61.3229 | 70 | ||
| 18 | 1.1250 | 64.46 | 113.6857 | 110 | -3% | 54.3282 | 64 | ||
| 19 | 1.1875 | 68.04 | 116.8571 | 114 | -2% | 47.1214 | 57 | ||
| 20 | 1.2500 | 71.62 | 119.5721 | 117 | -2% | 39.7306 | 50 | ||
| 21 | 1.3125 | 75.20 | 121.8201 | 120 | -1% | 32.1847 | 43 | ||
| 22 | 1.3750 | 78.78 | 123.5925 | 122 | -1% | 24.5130 | 36 | ||
| 23 | 1.4375 | 82.36 | 124.8823 | 124 | -1% | 16.7456 | 29 | ||
| 24 | 1.5000 | 85.94 | 125.6844 | 125 | -1% | 8.9129 | 22 | ||
| 25 | 1.5625 | 89.52 | 125.9957 | 126 | 0% | 1.0453 | 15 | ||
| 26 | 1.6250 | 93.11 | 125.8149 | 126 | 0% | -6.8263 | 8 |
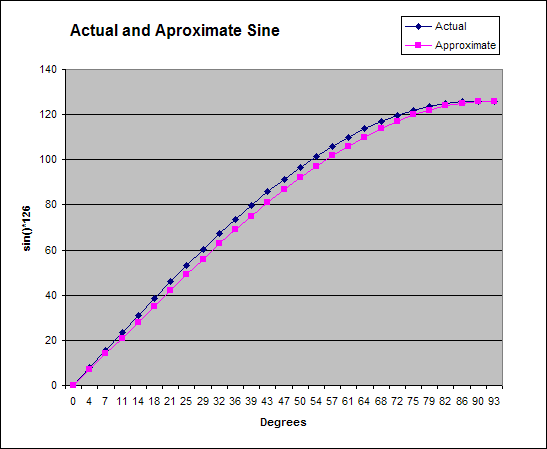
And the really nice thing is that unlike the original 6800 code, dividing by 16 for us takes only 2 instructions: swap nibbles and mask off the top one.
Code Generator output to Divide by 16:
; ACC = ACC * 0.0625 ; Temp = TEMP ; ACC size = 8 bits ; Error = 0.5 % ; Bytes order = little endian ; Round = no ; ALGORITHM: ; Clear accumulator ; Add input / 16 to accumulator ; Move accumulator to result ; ; Approximated constant: 0.0625, Error: 0 % ; Input: ACC0, 8 bits ; Output: ACC0, 4 bits ; Code size: 3 instructions ;shift accumulator right 4 times mov w, <>ACC0 and w, #$0F mov ACC0, w ; Generated by www.piclist.com/cgi-bin/constdivmul.exe (1-May-2002 version) ; Tue Apr 12 23:10:53 2005 GMT
So as a result, we can write a really short program than generates a first 26 steps of a 104 step sine without a table:
org $10 sine ds 1 cosine ds 1 RESET start start clr sine ;set sin to 0. This is actually -127 ; because we are working with signed values. mov w, #126 ;set cos to half way between 0 and 255. mov cosine, w ; this is actually +0. cycle mov w, <>cosine and w, #$0F add sine, w ;sine += cosine \ 16 mov w, <>sine and w, #$0F sub cosine, w ;cosine -= sine \ 16 jmp cycle
To generate a complete sine, reset sine and cosine every 16 steps or when cosine reaches 0. For the first 16 steps return sine+128 (i.e. with the high bit set), for the next 16 return cosine+128, then return 128-sine, and finish with 128-cosine.
org $10 sine ds 1 cosine ds 1 quadrant ds 1 RESET start start mov quadrant, #-1 quadcycle inc quadrant clr sine ;set sin to 0. This is actually -127 ; because we are working with signed values. mov w, #126 ;set cos to half way between 0 and 255. mov cosine, w ; this is actually +0. cycle mov w, <>cosine and w, #$0F add sine, w mov w, <>sine and w, #$0F sub cosine, w sc jmp quadcycle mov w, sine ;load the sine snb quadrant.0 ;if we are in the first or third quadrant mov w, cosine ; and the cosine for the 2nd or 4th. snb quadrant.1 ;for the second half cycle not w ; the value will be subtracted from 128 xor w, #128 ;see notes below: jmp cycle
So, in 14 instructions, we encoded a 104 step table. Not bad! Now, it is a little slower than a table lookup: Once through the loop is about 15 cycles on the average compaired to 5 or 6 for the average table lookup.
Notice how adding 128 is just setting bit 7 if the original value is less than 128 to start with. If the value is already negative (bit 7 is set and we are considering the value to be a signed byte i.e. between +127 and -128) then adding 128 will result in an overflow which will have the effect of clearing bit 7. So 128 + x or 128 - x can be managed by inverting X if it is to be subtracted and then toggleing bit 7.
It turns out that a divisor of 15 is a little bit better than 16 as you can see here:
Step |
Radians |
Degrees |
sin() |
~sin() |
error |
cos() |
~cos() |
||
| 0 | 0.0000 | 0.00 | 0.0000 | 0 | 0% | 126.0000 | 126 | Range: |
126 |
| 1 | 0.0625 | 3.58 | 7.8699 | 8 | 0% | 125.7540 | 126 | Divisor: |
15 |
| 2 | 0.1250 | 7.16 | 15.7090 | 16 | 0% | 125.0169 | 125 | Step: |
0.0625 |
| 3 | 0.1875 | 10.74 | 23.4868 | 24 | 0% | 123.7916 | 124 | ||
| 4 | 0.2500 | 14.32 | 31.1729 | 32 | 1% | 122.0830 | 122 | ||
| 5 | 0.3125 | 17.90 | 38.7373 | 40 | 1% | 119.8976 | 120 | ||
| 6 | 0.3750 | 21.49 | 46.1503 | 48 | 1% | 117.2440 | 117 | ||
| 7 | 0.4375 | 25.07 | 53.3832 | 55 | 1% | 114.1325 | 114 | ||
| 8 | 0.5000 | 28.65 | 60.4076 | 62 | 1% | 110.5754 | 110 | ||
| 9 | 0.5625 | 32.23 | 67.1961 | 69 | 1% | 106.5865 | 106 | ||
| 10 | 0.6250 | 35.81 | 73.7223 | 76 | 2% | 102.1814 | 101 | ||
| 11 | 0.6875 | 39.39 | 79.9605 | 82 | 2% | 97.3772 | 96 | ||
| 12 | 0.7500 | 42.97 | 85.8865 | 88 | 2% | 92.1928 | 91 | ||
| 13 | 0.8125 | 46.55 | 91.4771 | 94 | 2% | 86.6484 | 85 | ||
| 14 | 0.8750 | 50.13 | 96.7105 | 99 | 2% | 80.7656 | 79 | ||
| 15 | 0.9375 | 53.71 | 101.5662 | 104 | 2% | 74.5674 | 73 | ||
| 16 | 1.0000 | 57.30 | 106.0253 | 108 | 2% | 68.0781 | 66 | ||
| 17 | 1.0625 | 60.88 | 110.0704 | 112 | 2% | 61.3229 | 59 | ||
| 18 | 1.1250 | 64.46 | 113.6857 | 115 | 1% | 54.3282 | 52 | ||
| 19 | 1.1875 | 68.04 | 116.8571 | 118 | 1% | 47.1214 | 45 | ||
| 20 | 1.2500 | 71.62 | 119.5721 | 121 | 1% | 39.7306 | 37 | ||
| 21 | 1.3125 | 75.20 | 121.8201 | 123 | 1% | 32.1847 | 29 | ||
| 22 | 1.3750 | 78.78 | 123.5925 | 124 | 0% | 24.5130 | 21 | ||
| 23 | 1.4375 | 82.36 | 124.8823 | 125 | 0% | 16.7456 | 13 | ||
| 24 | 1.5000 | 85.94 | 125.6844 | 125 | -1% | 8.9129 | 5 | ||
| 25 | 1.5625 | 89.52 | 125.9957 | 125 | -1% | 1.0453 | -3 | ||
| 26 | 1.6250 | 93.11 | 125.8149 | 124 | -1% | -6.8263 | -11 |
Although dividing by 15 does require, 12 instructions vice 2.
If you really want to get crazy, you can do a 62 step quandrant of a 248 step sine using a divisor of 38. The maximum error is 4% and it takes 18 instructions for the divide by 38.
| file: /Techref/new/letter/news0404.htm, 60KB, , updated: 2012/10/23 16:53, local time: 2025/10/24 10:36,
owner: JMN-EFP-786,
216.73.216.20,10-1-5-169:LOG IN
|
| ©2025 These pages are served without commercial sponsorship. (No popup ads, etc...).Bandwidth abuse increases hosting cost forcing sponsorship or shutdown. This server aggressively defends against automated copying for any reason including offline viewing, duplication, etc... Please respect this requirement and DO NOT RIP THIS SITE. Questions? <A HREF="http://massmind.ecomorder.com/Techref/new/letter/news0404.htm"> Massmind Newsletter 04/04 - Sine Waves</A> |
| Did you find what you needed? |
Welcome to ecomorder.com! |
|
Ashley Roll has put together a really nice little unit here. Leave off the MAX232 and keep these handy for the few times you need true RS232! |
.